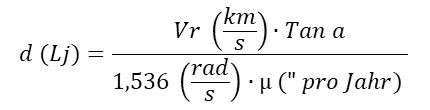Sternstromparallaxe

Die Sterne eines offenen Sternhaufens gehören tatsächlich zusammen; sie sind gravitativ aneinander gebunden, nehmen ein gemeinsames Raumgebiet ein und bewegen sich auch in die gleiche Richtung mit einer gleich großen Geschwindigkeit. Es sind aber auch Sterne in einem offenen Sternhaufen zu sehen, die nicht zu ihm gehören, sondern sich davor oder dahinter befinden. Solche Sterne nennt man Feldsterne. Feldsterne lassen sich leicht erkennen, da sie eine andere Eigenbewegung als die Haufenmitglieder haben.

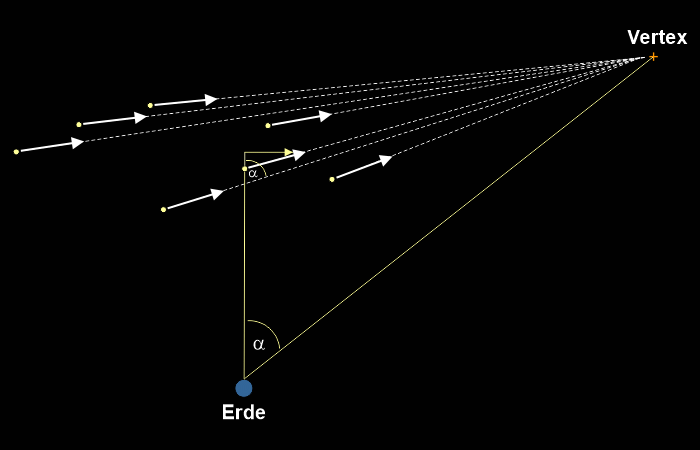
Alle Sterne eines offenen Sternhaufens bewegen sich am Himmel auf einen bestimmten Punkt zu, dem Fluchtpuinkt oder Vertex. Das ist aber ein perspektivischer Effekt, denn in Wirklichkeit bewegen sich die Sterne parallel zueinander. Das gleiche kann man beobachten, wenn parallele Eisenbahnschienen scheinbar am Horizont zusammenlaufen zu scheinen.

Durch den Fluchtpunkt erhält man die Bewegungsrichtung im Raum. Durch Bestimmung der Radialgeschwindigkeit, also die Bewegung eines Sterns auf uns zu oder von uns weg kann man zusammen mit der Messung der Eigenbewegung pro Jahr sowie dem Winkel Alpha die Entfernung des Sternhaufens berechnen. Diese Methode der Entfernungsbestimmung bezeichnet man als Sternstromparallaxe.

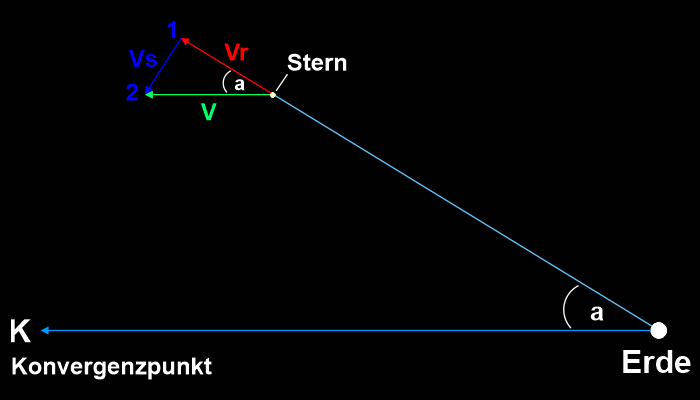
Wie wird das genau gemacht? Dazu betrachten wir die Grafik weiter unten. Der Beobachter blickt von der Erde aus rechts unten. Bei K befindet sich der Fluchtpunkt oder Vertex. Oben ist ein Stern eingezeichnet. Dieser bewegt sich auf der grünen Linie mit einer bestimmten Geschwindigkeit (V), also parallel zum Konvergentpunkt. Diese Sternbewegung verläuft aber nicht genau senkrecht zum Beobachter auf der Erde, sondern schräge zu ihm. Von der Erde aus sieht man nur die Bewegung senkrecht zum Beobachter auf der blauen Linie von Punkt 1 nach Punkt 2 (µ). Die Bewegung des Sterns vom Beobachter weg (Vr) auf der roten Linie ist von der Erde aus nicht zu sehen. Man bezeichnet Vr auch als Radialgeschwindigkeit. Die Radialgeschwindigkeit kann man aber sehr genau messen in Kilometern pro Sekunde mit Hilfe der Spektrallinien des Sterns unabhängig von seiner Entfernung. Damit kennen wir schon mal die wahre Geschwindigkeit Vr.

Die drei Linien rot, blau und grün bilden ein rechtwinkliges Dreieck, das Geschwindigkeitsdreieck. Den Winkel a zwischen der roten und der grünen Linie kann man messen, denn das ist der Winkelabstand vom Stern zum Konvergenzpunkt. Damit sind drei Größen bekannt: Der Winkel a, die Geschwindigkeit Vr in Kilometer pro Sekunde und der Winkel zwischen Vr (rot) und Vs (blau) ist ein rechter. Damit können wir die wahre Geschwindigkeit Vs berechnen.

In einem rechtwinkligen Dreieck gilt:

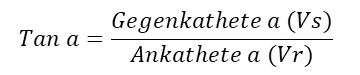
Der Tangens des Winkels a ist das Verhältnis von der Gegenkathete (Vs) zur Ankathete (Vr). Wir brauchen also nur den Tangens vom Winkel a auszurechnen und das Ergebnis mit dem Wert von Vr (Kilometer pro Sekunde) zu multiplizieren.

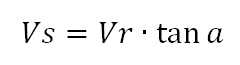
Die Angabe der Geschwindigkeit Vs ist ebenfalls in Kilometer pro Sekunde. Von der Erde aus kann man nur die scheinbare Winkelgeschwindigkeit in Bogenmaß senkrecht zur Sichtlinie µ bestimmen. Kennt man aber neben der scheinbaren auch die wahre Geschwindigkeit Vs, die wie eben gezeigt berechnet wird, kann man daraus die Entfernung d berechnen. Die Formel dazu lautet:

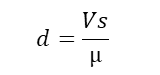
Hier gibt es aber ein Problem mit den Einheiten: Die Angabe Vr ist in Kilometern pro Sekunde (km/s), die Eigenbewegung wird aber in Bogensekunden pro Jahr gemessen. Dafür ist eine Anpassung erforderlich. Man benutzt dazu das Bogenmaß pro Sekunde (rad/s). In der Literatur findet man eine fertige Formel, wo man für µ die Eigenbewegung in Bogensekunden pro Jahr eingibt und die Entfernung d in Lichtjahren erhält:

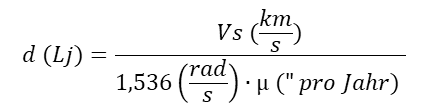
Man kann sich den Zwischenschritt zur Berechnung von Vs auch sparen und diesen gleich in die Formel mit einbauen: